কোণ কাকে বলে । কোণ পরিমাপের একক ও পদ্ধতি । কোণের বৈশিষ্ট্য ও প্রকারভেদ

কোণ কাকে বলে । কোণ পরিমাপের একক ও পদ্ধতি ।  কোণের বৈশিষ্ট্য ও প্রকারভেদ

আপনারা যারা কোণ কাকে বলে? কোণ কত প্রকার ? কোণ কত প্রকার ও কী কী? কোণ পরিমাপের একক কি?  কোণ পরিমাপের একক কত প্রকার? কোণ পরিমাপের পদ্ধতি কয়টি? কোণের বৈশিষ্ট্য কি কি? কোণের একক কি? কোণের সংজ্ঞা? কোণের বৈশিষ্ট্য? কোণের শীর্ষবিন্দু কাকে বলে? কোণের প্রকারভেদ ইত্যাদি কোণ বিষয়ক পরিপূর্ণ ধারণা নিতে চান তাদের জন্য আজকের আলোচনা।

চিত্র: (১)  কোণ

কোণ হলো দুটি রেখার মধ্যে তৈরি হওয়া স্থান। দুইটি রেখার উভয় পাশের মধ্যবিন্দুকে একসাথে যুক্ত করে একটি কোণ তৈরি হয়। কোণের সাধারণ চিহ্ন হল "∠"। কোণ হলো একটি জ্যামিতিক আকার । কোণ ব্যাসিক জ্যামিতি এবং ট্রিগোনোমেট্রির একটি মৌলিক ধারণা।কোণের মান বিভিন্ন পদ্ধতিতে প্রকাশ করা যায়, যেমন- ডিগ্রি বা রেডিয়ান। কোণের মান শূন্য (০)  থেকে ৩৬০ ডিগ্রি পর্যন্ত হতে পারে। এছাড়া কোণের বৈশিষ্ট্য হতে দেখা যায় কোন কোণই সমান নয় বা একই প্রকার নয় কারণ তাদের আকার এবং মান পার্থক্যমূলক হতে পারে। আজকের আলোচনায় কোণ কাকে বলে?  কোণের সংজ্ঞা ও কোণের বৈশিষ্ট্য একই সাথে কোণ পরিমাপের একক, পদ্ধতি ও কোণের চিত্র নিয়ে আলোচনা করা হবে। আশা করি শেষ পর্যন্ত পড়বেন।

{tocify} Stitle={Custom Title}}

কোণ কাকে বলে?

কোণ বলতে বোঝায় দুটি সরলরেখার মধ্যে গঠিত একটি চিহ্নিত বিন্দু, যা সাধারণত ডিগ্রি বা রেডিয়ানে প্রকাশ করা হয়। একটি কোণের আকার হল দুটি সরলরেখার মধ্যে গঠিত কোণ। একই সমতলে অবস্থিত দুইটি রশ্মির প্রান্তবিন্দু একই হলে কোণ তৈরি হয়। অর্থাৎ, কোণের সংজ্ঞা হলো  একই সমতলে অবস্থিত দুইটি রশ্মির প্রান্তবিন্দুর মিলনস্থানকেই কোণ বলে।

কোণ একটি জ্যামিতিক চিহ্নিত দশাংশিক সংখ্যা হিসাবে প্রকাশ করা হয়। একটি কোণ সাধারণত দুটি সরলরেখার উপর অবস্থিত বিন্দু দ্বারা চিহ্নিত হয়। কোনো বিন্দুকে কোণের চিহ্ন দিয়ে নির্দেশ করা হয়। উদাহরণস্বরূপ, একটি কোণ যেমন ABC হলে, এখানে B বিন্দুকে কোণের চিহ্ন দিয়ে নির্দেশ করা হবে। কোণের চিহ্ন সাধারণত কেমন হয় তা প্রকাশ করার জন্য সাধারণত কোণের নামের সাথে একটি ছোট বাঁকা চিহ্ন ব্যবহার করা হয়। উদাহরণস্বরূপ, কোণ ABC হলে, এর চিহ্ন হবে ∠ABC।  (চিত্র-১)

রশ্মি দইটিকে কোণের বাহু বলে। এখনে, BC এবং AB রশ্মি দুইটি ∠ABC এর বাহু।
রশ্মি ‍দুইটির সাধারণ বিন্দুকে শীর্ষবিন্দু বলে। এখানে, B বিন্দুটি ∠ABC এর শীর্ষবিন্দু। {alertSuccess}

কোণ কত প্রকার?

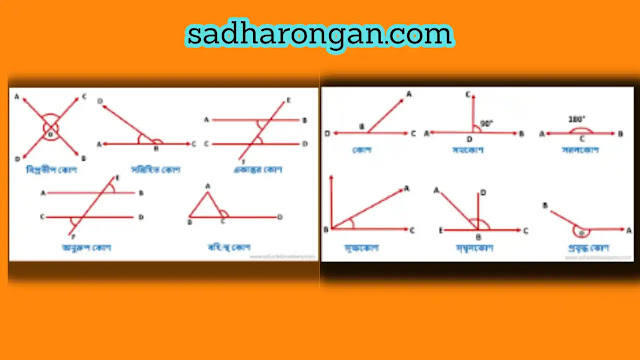
কোণের নির্দিষ্ট কোনো প্রকারভেদ নাই। কোণ বহু প্রকার হতে পারি। মৌলিক গণিতে যেসকল কোণের বর্ণনা পাওয়া যায় সেগুলোকে নিম্নোক্তভাবে বর্ণনা করা যেতে পারে।

সমকোণের ভিত্তিতে কোণের প্রকারভেদ

• সমকোণ ( right angle )
• সরলকোণ ( straight angle )
• সূক্ষ্মকোণ ( obtuse angle )
• স্থূলকোণ ( acute angle )
• প্রবৃদ্ধ কোণ ( reflex angle )

দুইটি কোণের সমষ্টির ভিত্তিতে কোণের প্রকারভেদ

• পূরক কোণ ( complementary angle )
• সম্পূরক কোণ ( Supplementary angle )
• সন্নিহিত কোণ ( adjacent angle )

দুইটি সরলরেখার ছেদকের ভিত্তিতে কোণের প্রকারভেদ

• বিপ্রতীপ কোণ ( vertical angle  )
• সমান্তরাল সরলরেখার ভিত্তিতে কোণের প্রকারভেদ
• একান্তর কোণ ( Alternate angle )
• অনুরূপ কোণ ( Corresponding angle )

ত্রিভুজক্ষেত্রের ভিত্তিতে কোণের প্রকারভেদ

• বহিঃস্থ কোণ ( Exterior angle )
• অন্তঃস্থ কোণ ( Interior angle )
• উন্নতি কোণ ( Angle of improvement )
• অবনতি কোণ ( angle of declination )
• শিরঃকোণ ( head angle )

বৃত্তক্ষেত্র এর ভিত্তিতে কোণের প্রকারভেদ

• কেন্দ্রস্থ কোণ ( Central angle )
• বৃত্তস্থ কোণ ( Inscribed angle )
• অর্ধবৃত্তস্থ কোণ ( semicircular angle )

এছাড়া অন্যান্য বিশেষ কোণের প্রকারভেদ

• শূন্য কোণ ( zero angle )
• পূর্ণ কোণ ( full angle )
• বিপরীত কোণ ( opposite angle )

কোণ পরিমাপের একক কি?

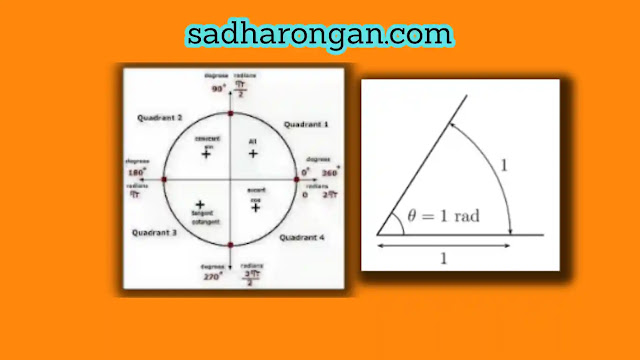
কোণ পরিমাপের একক রেডিয়ান (radian) বা ডিগ্রি (degree) । এই দুটি পরিমাপের মধ্যে সম্পূর্ণ কোণ একটি একক এর সমান। তবে কোন কোন অবস্থায় একটি পরিমাপের ব্যবহার উপযোগী হবে সেটি নির্ভর করে তথ্যের ধরন এবং ব্যবহারের ক্ষেত্রে। একটি বৃত্তের ব্যাসার্ধের সমান দৈর্ঘ্যের একটি বৃত্তচাপ বৃত্তের কেন্দ্রে যে কোণ উৎপন্ন করে, তাকে এক রেডিয়ান বলা হয়। একটি পূর্ণ বৃত্তের সাথে একটি পূর্ণ ঘুরানো কোণের মান 2π রেডিয়ান হয়, যা প্রায় 6.28 রেডিয়ান। ডিগ্রি হল একটি কোণের পরিমাপের একক, যা বৃত্তের পূর্ণকোণের 360 টি সমান অংশে ভাগ করা হয়। এক ডিগ্রির মান π/180 রেডিয়ান।বিভিন্ন গণিত ও পদার্থবিদ্যার ক্ষেত্রে রেডিয়ান ও ডিগ্রি উভয় একক ব্যবহৃত হয়।

কোণ পরিমাপের পদ্ধতি কয়টি?

সরলরেখার দুটি কোণের মান নির্ণয় করার জন্য সাধারণত তিনটি পদ্ধতি ব্যবহার করা হয়।

ডিগ্রী পদ্ধতি:

এখানে কোণের মান সাধারণত ডিগ্রীতে প্রকাশ করা হয়। ১ ডিগ্রীর সমান 60 মিনিট এবং ১ মিনিটের সমান 60 সেকেন্ড ধরে নেওয়া হয়।

ডিগ্রী পদ্ধতি হল একটি কোণ মাপার পদ্ধতি, যেখানে পূর্ণ ঘূর্ণন বা চার সমান খন্ড মেরে কোনটি ঘুরে আসে সেটি হল 360 ডিগ্রী। এই পদ্ধতিতে কোন একটি কোণ মাপার জন্য একটি বৃত্তের কেন্দ্র থেকে দুইটি রেখার মধ্যে কোণটির মাপ হিসাব করা হয়। সেই বৃত্তের কেন্দ্র হল কোণটির শীর্ষবিন্দু।

ডিগ্রী পদ্ধতিতে কোন কোণের মান নির্দিষ্ট করার জন্য, সেটি ডিগ্রী চিহ্নিত করে লিখা হয়, যেমন 30° কোণ। এই পদ্ধতিতে কোন কোণের মান নির্দিষ্ট করার জন্য একটি প্রোট্র্যাকশন ব্যবহার করা হয়, যেমন ক্লকওয়াইজের ঘড়ি ব্যবহার করে সমস্ত কোণের মান নির্ণয় করা যায়।

রেডিয়ান পদ্ধতি: 

এখানে কোণের মান রেডিয়ান নামে একটি এককে প্রকাশ করা হয়। একটি কোণের মান রেডিয়ান পদ্ধতিতে নির্ণয় করার জন্য কোণের কেন্দ্রবিন্দুতে একটি বৃত্ত তৈরি করা হয় এবং বৃত্তের ব্যাস রেডিয়ান হিসেবে নির্ণয় করা হয়।

রেডিয়ানে কোণের মান নির্ণয় করার সূত্র হল:

রেডিয়ান = কোণের ব্যাস / কোণের কেন্দ্রবিন্দু থেকে সরলরেখার দুরত্ব

অর্থাৎ, একটি কোণের রেডিয়ান হলো সেই কোণের ব্যাস এবং কেন্দ্রবিন্দু থেকে সরলরেখার দুরত্বের অনুপাত।

উদাহরণ সাধারণ করে বলা যাক, যদি কোন কোণের ব্যাস ৩ ইঞ্চি হল এবং কেন্দ্রবিন্দু থেকে সরলরেখার দুরত্ব ২ ইঞ্চি হল তবে কোণটির রেডিয়ান হবে:

রেডিয়ান = 3 / 2 = 1.5 এই রেডিয়ান মান একটি কোণ নির্দিষ্ট করতে ব্যবহৃত হয়।

গ্রেড পদ্ধতি: 

এখানে কোণের মান গ্রেড নামে একটি এককে প্রকাশ করা হয়। কোণের পরিমাপের গ্রেড পদ্ধতি হল একটি পদ্ধতি যা অধিকতর জ্যামিতিক ক্ষেত্রে ব্যবহৃত হয়। এই পদ্ধতিতে কোণের মানকে অংকের মাধ্যমে প্রকাশ করা হয়।এখানে ১ গ্রেডের সমান ৯০ ডিগ্রী ধরে নেওয়া হয়। কোণ পরিমাপের গ্রেড পদ্ধতি হল একটি কোণ মাপার পদ্ধতি, যেখানে কোন একটি কোণকে স্থানান্তর করে সমান দুটি কোণ বের করা হয়। এই পদ্ধতিতে সমান কোণগুলোর সংখ্যা হল ৪ টি, যা হল G1, G2, G3 এবং G4।

G1 এবং G3 একই সাইডের একই কোণে থাকা এবং একটি স্থির বিন্দুতে দুটি সরল রেখার মধ্যে তৈরি হয়। একটি স্থির বিন্দুতে দুটি সরল রেখার মধ্যে কোনটি প্রথমে আসে তাকে G1 বলে এবং অন্যটি তার সাথে সমান কোণ তৈরি করে তাকে G3 বলে।

G2 এবং G4 পরের কোণে থাকা এবং একটি স্থির বিন্দুতে তিনটি সরল রেখার মধ্যে তৈরি হয়। তিনটি সরল রেখার মধ্যে সমান কোণ তৈরি করে তাকে G2 বলে এবং তিনটি সরল রেখার মধ্যে সমকোণী কোণ তৈরি করে তাকে G4 বলে।

সবচেয়ে সাধারণভাবে ডিগ্রী ব্যবহার করা হয় কোণের মান নির্ণয়ের জন্য।{alertSuccess}

রেডিয়ান কোণ ও ডিগ্রি কোণের সম্পর্ক

রেডিয়ান এবং ডিগ্রি উভয়ই কোণের মান নির্ণয় করার জন্য ব্যবহৃত একক। তবে এদের মধ্যে একটি গঠনমূলক পার্থক্য রয়েছে।

ডিগ্রি কোণের মান নির্ণয় করার জন্য কোণের ব্যাস সম্পর্কে কথা বলা হয়। এখানে একটি পূর্ণ চক্রের ৩৬০ ডিগ্রি হল কোণটির মান। এক ডিগ্রি সমতা ১/৩৬০ এর সমান। যেমন, ৯০ ডিগ্রি হল ১/৪ চক্র বা পরিপূর্ণ কোণের চতুর্থাংশ।

আবার, রেডিয়ান কোণের মান নির্ণয় করার জন্য ব্যবহৃত হয় বৃত্তের ব্যাস সম্পর্কে। এখানে এক পূর্ণ চক্রে রেডিয়ানের মান ২ π। এর মান একটি ডিগ্রি কোণের মান এর সমান হওয়ার জন্য মৌলিক রূপে বের করা হয় যা হল:
রেডিয়ান = (π/১৮০) * ডিগ্রি

এখন যদি কোন কোণের মান ডিগ্রি হিসেবে দেওয়া থাকে তবে সেটি রেডিয়ানে পরিণত করতে হলে নিম্নোক্ত সূত্র ব্যবহার করতে হবে:
রেডিয়ান = (π/১৮০) * ডিগ্রি

এখন একটি উদাহরণ দেখা যাক। যদি কোন কোণের মান ৪৫ ডিগ্রি হয় তবে সেটি রেডিয়ানে পরিণত করতে হবে:
রেডিয়ান = (π/১৮০) * ৪৫
বা, রেডিয়ান = ০.৭৮৫৪

তাই কোণের মান রেডিয়ান বা ডিগ্রি হিসেবে উভয়ই নির্দিষ্ট করা যায়, তবে গণিতে রেডিয়ান ব্যবহার করা বেশি সম্ভবত কারণ সেটি গণিত অপারেশন করতে সহজ হয়।

কোণের বৈশিষ্ট্য:

• কোণ স্থানাংক দিয়ে নির্দেশ করা হয়। সাধারণত কোণের স্থানাংক একটি বর্ণের মাধ্যমে প্রকাশ করা হয়। উদাহরণস্বরূপ, একটি সাধারণ কোণের স্থানাংক হতে পারে A বা ∠A।
• কোণ দুটি রশ্মির বা সরলরেখার মাধ্যমে গঠিত হয়।
• একটি কোণের সর্ব্বোচ্চ মান ৩৬০ ডিগ্রি।
• প্রত্যেক বিপ্রতীপ বা একান্তর বা অনুরূপ কোন জোড়া পরস্পর সমান।
• অর্ধবৃত্তস্থ কোণের মান এক সমকোণ।
• কোণের আকার মধ্যবিন্দু থেকে পরিবর্তিত হয় না।
• কোণ মাপ করা হয় মানে ডিগ্রি বা রেডিয়ান এককে।
• একটি সমকোণী ত্রিভুজে উন্নতি কোণ ও অবনতি কোণদ্বয় পরস্পর সমান হয়।
• ত্রিভুজের তিনটি কোণের সমষ্টি সর্বদা ১৮০ ডিগ্রি।
• কোণের দুটি সমকোণের যোগফল ৩৬০ ডিগ্রি বা পূর্ণকোণ।
• কোণ একটি স্থির আকার।

আজকের আলোচনায় কোণের সংজ্ঞা, প্রকারভেদ, নাম, কোণ পরিপাপের একক পদ্ধতি ও তাদের মধ্যে সম্পর্কসহ কোণের বিভিন্ন বৈশিষ্ট্য সম্পর্কে আলোচনা করা হয়েছে। আশা করি উপকৃত হয়েছেন। ভালো লাগলে শেয়ার ও কমেন্ট করে পাশে থাকবেন। ধন্যবাদ।